LA TOPOLOGIA O MATEMÁTICA RELACIONAL:
La topología se ha constituido en una ciencia (derivada
de las matemáticas) que está modelando el mundo mostrándolo tal y como es, con
la ventaja de que sus figuras y representaciones topológicas traen consigo una
expresión matemática que permite comprender mejor su estructura y como ésta
puede ser sometida a cambios sin que se llegue alterar la forma de los objetos
de la realidad. Uno de los campos más prolíficos en los que los matemáticos han
hecho su auge y que ya constituye una de las mayores aportaciones a la ciencia,
tiene que ver con el Procesamiento de Imágenes Digitales 3D.Procesamiento de
imágenes digitales 3D.
Matemática
relacional (Topología)
La matemática relacional es la
rama de las matemáticas dedicada al estudio de aquellas propiedades de los cuerpos
geométricos que permanecen inalteradas por transformaciones continuas. Es una
disciplina que estudia las propiedades de los espacios topológicos y las
funciones continuas. La Topología se interesa por conceptos como proximidad,
número de agujeros, el tipo de consistencia (o textura) que presenta un objeto,
comparar objetos y clasificar. La matemática relacional o Topología ha sido
reconocida como un área particular de las matemáticas en los últimos 50 años, y
su principal crecimiento se ha originado dentro de los últimos 30 años. Incluye
campos no métricos tales como las teorías de las redes y de las gráficas. Es
una de las nuevas ramas de las matemáticas que ha demostrado más poder y ha
producido fuertes repercusiones en la mayoría de las antiguas ramas de esta
ciencia y ha tenido también efecto importante en las otras ciencias, incluso en
las ciencias sociales.
Partió como una respuesta a la
necesidad del análisis clásico del cálculo y de las ecuaciones diferenciales.
Sin embargo la topología no es una rama del análisis sino una especie de
geometría, una geometría más bien de pensamiento geométrico basado en la prueba
de la existencia de un cierto teorema, en campos tales como las redes, los
gráficos, los conjuntos. Su aplicación al estudio de las interacciones entre
las partes de los sistemas (sociales o de otro tipo) es evidente, por ejemplo
L. Spier expresa la teoría de los gráficos como un método para comprender la
conducta administrativa. Esta es una gran ayuda para ilustrar las propiedades
estructurales de un problema administrativo, o de una estructura organizacional
y las propiedades de las conexiones entre las partes de un sistema.
Aplicaciones
de la topología en la ingeniería:
La búsqueda permanente por
parte de los científicos de una representación gráfica de los diferentes
fenómenos que nos presenta la naturaleza día tras día; esto con el fin de
comprender mejor ciertos comportamientos, precisa por parte de éstos a recurrir
a distintas ciencias con el fin de que se provea de esa representación. Para
ello los matemáticos modernos han lanzado al ruedo una de los más complejas e
interesantes postulados que se hayan formulado en los últimos tiempos a
propósito del desarrollo de las matemáticas y su acostumbrado desarrollo de la
mano con la ciencia.
Ejemplos:
Para hablar de topología o
matemática relacional hay que hablar de diferentes ejemplos gráficos, visuales
y demostración lógica tratare de mostrar los diferentes ejemplos brevemente
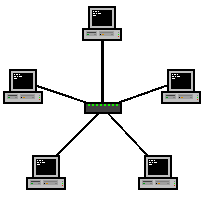
Aplicación a un sistema de redes:
Aquí tenemos un sencillo ejemplo aplicando tipología
para resolver un poner en funcionamiento su sistema de redes en la topología geométrica
de estrella.
Una red en estrella es
una red en la cual las estaciones están conectadas directamente a un punto
central y todas las comunicaciones se han de hacer necesariamente a través de
éste.
Dado su transmisión, una red en estrella activa
tiene un nodo central activo que normalmente tiene los medios
para prevenir problemas relacionados con el eco.
Ejemplo
topología aplicada a transformación de formas:
Esta es la parte de la topología donde está
permitido está permitido doblar, estirar, encoger, retorcer... los objetos pero
siempre que se haga sin romper ni separar lo que estaba unido (la
transformación debe ser continua) ni pegar lo que estaba separado (la inversa
también debe ser continua). Por ejemplo, en topología un círculo es lo mismo
que un cuadrado, ya que podemos transformar uno en otro de forma continua, sin
romper ni pegar.
En este ejemplo podemos observar que partimos
de una figura en forma de dona donde aplicando cada tipo trasformación de
formas sin cortar en ningún momento ni dañar la figura podemos cambiar a una
forma que nos sirva para una solución es muy útil usar la trasformación como
parte de los sistemas partiendo del anterior.
Teorías:
-Teoría de grafos:
Es necesario
pues, entenderse los grafos como un conjunto de puntos, y las aristas son las
líneas. A través del cual se interconectan los vértices.
A partir del
problema de los siete puentes de Konisberg, y consistía en saber si era posible
si se podía recorrer la ciudad atravesando una vez cada punto. Para lo que se
representa a la ciudad usando grafos. De esta forma se estableció que:
Un grafo es
CONEXO si existe un camino entre los vértices.
Un grafo es
EULERIANO si existe pasa por cada arista solo una vez.
Se utiliza
para representar circuitos eléctricos y para realizar cálculos sobre las
partículas elementales.

Se considera
un nudo como una curva continua y cerrada, sin puntos dobles. Es posible
realizarle cualquier deformación pero no cortes. Tiene como objetivo determinar
cuando los nudos son equivalentes, es decir, que se pueden pasar de uno al otro
Existen,
diferentes nudos por ejemplo,
Nudo
trivial, nudo trébol y nudo figura de ocho. Entre ellos se pueden realizar todo
tipo de operaciones matemáticas
Con la
teoría de nudos, se ha descrito de una mejor manera las fuerzas principales
como la gravedad, electromagnetismo y los tipos de interacciones entre
partículas.
-Teoría de superficies
Existe pues
una clasificación de superficies según la topología, con diversidad de
dimensiones. Por ejemplo el plano, la esfera y el toro. Estas a su vez pueden
ser cerradas y acotadas.
Además, teóricamente hablando
la topología profundamente explicado a partir de las matemáticas se puede
encontrar en, realizado por TEC (La señal de la ciencia).
PRINCIPIOS DE LA TEORÍA GENERAL DE SISTEMAS:
-Integridad y Totalidad:
“Un sistema no está hecho de partes independientes sino de partes interdependientes, por lo tanto un sistema no es la suma total de sus partes sino que es caracterizado por su unidad y su todismo”.
Cada sistema es una totalidad, pero al mismo tiempo se reconoce como una parte integrada y correlacionada dentro de una totalidad más amplia con la que se comunica circularmente.
La familia es un sistema total, integrado, por ello todo cambio que se produce a nivel individual causa cambios a otros niveles del sistema.
“Un sistema no está hecho de partes independientes sino de partes interdependientes, por lo tanto un sistema no es la suma total de sus partes sino que es caracterizado por su unidad y su todismo”.
Cada sistema es una totalidad, pero al mismo tiempo se reconoce como una parte integrada y correlacionada dentro de una totalidad más amplia con la que se comunica circularmente.
La familia es un sistema total, integrado, por ello todo cambio que se produce a nivel individual causa cambios a otros niveles del sistema.
Si
es importante que un miembro de la familia cambie, es imprescindible que el
sistema cambie.
Si un hijo sufre o se enferma, su síntoma se produce en el sistema.
Si un hijo sufre o se enferma, su síntoma se produce en el sistema.
Totalidad
“Cada una de las partes de un sistema están relacionadas de tal modo con las otras que un cambio en una de ellas provoca un cambio en todas las demás y en el sistema total”.
“Un sistema se comporta no sólo como simple compuesto de elementos interdependientes, sino como un todo inseparable y coherente”.
“Un sistema no puede entenderse como la suma de sus partes; un análisis formal de los elementos artificialmente aislados destruiría el objeto mismo de una visión sistémica por lo que es necesario dejar de lado el concepto de Gestalt y empezar a tomar mayor atención al concepto de organización”.
Jerarquía
La manera en que se organiza un sistema es a través de jerarquías. Un sistema complejo incluye un número de subsistemas.
“Cualquier sistema consiste de varias partes individuales, cada una de ellas es fundamental y tiene relación con las otras partes para alcanzar un cierto resultado; cada una actúa como un estímulo para las otras partes. El sistema tiene un orden y una secuencia, la cual estará determinada por las acciones, respuestas e interacciones entre las partes. Esta interacción constante determina como se manifestará el sistema. Un Sistema sólo tiene vida en el momento, cuando sus partes componentes se encuentran presentes.
Equifinalidad y Equicausalidad.
Estos conceptos sistémicos revolucionaron los paradigmas lineales, aristotélicos y psicoanalíticos.
La noción de Equifinalidad alude al hecho de que u sistema puede alcanzar el mismo estado final a partir de condiciones iniciales distintas, lo contrario a buscar una causa única del problema.
En la Equicausalidad, se refiere a que la misma condición inicial puede dar lugar a estados finales distintos.
Equifinalidad
En un sistema circular y automodificador los resultados no están determinados tanto por las condiciones iniciales como por la naturaleza del proceso o los parámetros del sistema. Este principio de Equifinalidad significa que idénticos resultados pueden tener orígenes distintos, porque lo decisivo es la naturaleza de la decisión es decir, como se relacionan los distintos elementos del sistema en un tiempo...en una historia.
Así, en el análisis del modo en que las personas se afectan unas a otras en su interacción, consideraremos que las características de los genes o el producto son mucho menos importantes que la organización de la interacción.
Por tanto, cuando observamos un sistema no se puede hacer necesariamente una inferencia con respecto a su estado pasado o futuro a partir de su estado actual, porque las mismas condiciones iniciales no producen los mismos efectos.
Por ejemplo, si tenemos:
Sistema A: 4x3+6=18
Sistema B: 2x5+8=18
Aquí observamos que el sistema “A” y el sistema “B” tienen inicios diferentes (4) y (“), y que, cada uno, tiene elementos diferentes al otro. Sin embargo, el resultado final es el mismo (18).
https://prezi.com/eqcnsrl1kgvp/topologia-o-matematica-relacional/
INGENIERÍA DE SISTEMAS:
Comprende la concepción, el planteamiento la evaluación y la
construcción científica de sistemas hombre - máquina. El interés teórico de
este campo se encuentra en el hecho de que aquellas entidades cuyos componentes
son heterogéneos (hombres, máquinas, materiales, dinero, edificios y otros
objetos, flujos de materias primas, flujo de producción, etc.) pueden ser
analizados como sistemas o se les puede aplicar el análisis de sistemas.
Ingeniería de
Sistemas es la aplicación de las ciencias matemáticas y físicas para
desarrollar sistemas que utilicen económicamente los materiales y fuerzas de la
naturaleza para el beneficio de la humanidad.
Una definición
especialmente completa -y que data de 1974- nos la ofrece un estándar militar
de las fuerzas aéreas estadounidenses sobre gestión de la ingeniería.
Ingeniería de Sistemas es la aplicación de esfuerzos científicos y de
ingeniería para:
(1) transformar
una necesidad de operación en una descripción de parámetros de rendimiento del
sistema y una configuración del sistema a través del uso de un proceso
iterativo de definición, síntesis, análisis, diseño, prueba y evaluación;
(2) integrar
parámetros técnicos relacionados para asegurar la compatibilidad de todos los
interfaces de programa y funcionales de manera que optimice la definición y
diseño del sistema total;
(3) integrar
factores de fiabilidad, mantenibilidad, seguridad, supervivencia, humanos y
otros en el esfuerzo de ingeniería total a fin de cumplir los objetivos de
coste, planificación y rendimiento técnico.
Ingeniería de
sistemas es un modo de enfoque interdisciplinario que permite estudiar y
comprender la realidad, con el propósito de implementar u optimizar sistemas
complejos. Puede verse como la aplicación tecnológica de la teoría de sistemas
a los esfuerzos de la ingeniería, adoptando en todo este trabajo el paradigma
sistémico. La ingeniería de sistemas integra otras disciplinas y grupos de
especialidad en un esfuerzo de equipo, formando un proceso de desarrollo
estructurado.
Una de las
principales diferencias de la ingeniería de sistemas respecto a otras
disciplinas de ingeniería tradicionales, consiste en que la ingeniería de
sistemas no construye productos tangibles. Mientras que los ingenieros civiles
podrían diseñar edificios o puentes, los ingenieros electrónicos podrían
diseñar circuitos, los ingenieros de sistemas tratan con sistemas abstractos
con ayuda de las metodologías de la ciencia de sistemas, y confían además en
otras disciplinas para diseñar y entregar los productos tangibles que son la
realización de esos sistemas.
Otro ámbito que
caracteriza a la ingeniería de sistemas es la interrelación con otras
disciplinas en un trabajo transdisciplinario.
Ámbito:
Esta área
comenzó a desarrollarse en la segunda parte del siglo XX con el veloz avance de
la ciencia de sistemas. Las empresas empezaron a tener una creciente aceptación
de que la ingeniería de sistemas podía gestionar el comportamiento impredecible
y la aparición de características imprevistas de los sistemas (propiedades
emergentes). Las decisiones tomadas al comienzo de un proyecto, cuyas
consecuencias pueden no haber sido entendidas claramente, tienen una enorme
implicación más adelante en la vida del sistema.
Un ingeniero de
sistemas debe explorar estas cuestiones y tomar decisiones críticas. No hay
métodos que garanticen que las decisiones tomadas hoy serán válidas cuando el
sistema entre en servicio años o décadas después de ser concebido, pero hay
metodologías que ayudan al proceso de toma de decisiones. Ejemplos como la
metodología de sistemas blandos (Soft Systems Methodology), la dinámica de
sistemas, modelo de sistemas viables (Viable System Model), teoría del Caos,
teoría de la complejidad, y otros que también están siendo explorados,
evaluados y desarrollados para apoyar al ingeniero en el proceso de toma de
decisiones.
RELACIÓN CON LA TGS:
1. Aplicación de las ciencias matemáticas para desarrollar sistemas que utilicen los materiales y fuerzas de la naturaleza para el beneficio de la humanidad.
http://en.wikipedia.org/wiki/Systems_theory#Systems_engineering
RELACIÓN CON LA TGS:
1. Aplicación de las ciencias matemáticas para desarrollar sistemas que utilicen los materiales y fuerzas de la naturaleza para el beneficio de la humanidad.
2. Promueve en las empresas cambios
que contribuyan al mejoramiento de estas.
3. Los ingenieros de sistemas son
capaces de tratar información y de
utilizar recursos cognitivos como la percepción, la memoria o el procesamiento
de información.
4. Viene a ser el resultado de gran
parte del movimiento de investigación general de los sistemas.
5.Es vista como una teoría matemática
convencional, un tipo de pensamiento, una ordenación de acuerdo a niveles de teorías.
6. Sirve para modelar objetos,
naturales o artificiales, simples o complejos, existentes o por aparecer.
http://en.wikipedia.org/wiki/Systems_theory#Systems_engineering
ANÁLISIS
FACTORIAL:
Es una técnica estadística de reducción de datos usada para explicar las correlaciones entre las variables observadas en términos de un número menor de variables no observadas llamadas factores.

Prácticamente
hasta los comienzos del siglo XX, el problema de las aptitudes había sido
objeto de puras especulaciones; la observación e introspección -poco o nada
sistematizadas, con frecuencia- han sido y siguen siendo incapaces de ofrecer
una prueba científica de la existencia de las aptitudes. Hoy en día, por
supuesto, se prefiere utilizar conceptos directamente derivados de actividades
mensurables de los seres humanos.
Para averiguar
experimentalmente cuáles son las características fundamentales de las funciones
cognoscitivas, se dispone, desde principios del siglo XX, de dos nuevos
instrumentos: el coeficiente de correlación y los “tests” mentales, y de un
concepto empírico: el de “unidad funcional”.
El Análisis
Factorial es una técnica que consiste en resumir la información contenida en
una matriz de datos con V variables. Para ello se identifican un reducido
número de factores F, siendo el número de factores menor que el número de
variables. Los factores representan a las variables originales, con una pérdida
mínima de información.
El modelo
matemático del Análisis Factorial es parecido al de la regresión múltiple. Cada
variable se expresa como una combinación lineal de factores no directamente
observables. A saber:
Xij = F1i•ai1 +
F2i•ai2 +....+ Fki•aik + Vi
siendo:
Xij la
puntuación del individuo i en la variable j .
Fij son los
coeficientes factoriales.
aij son las
puntuaciones factoriales.
Vi es el factor
único de cada variable.
Se asume que los
factores únicos no están correlacionados entre sí ni con los factores comunes.
Así mismo, podemos distinguir entre:
Análisis
Factorial Exploratorio, donde no se conocen los factores "a priori",
sino que se determinan mediante el Análisis Factorial.
Análisis
Confirmatorio donde se propone "a priori" un modelo según el cual hay
unos factores que representan a las variables originales, siendo el número de
éstos superior al de aquellos, y se somete a comprobación el modelo.
Para que el
Análisis Factorial tenga sentido deberían cumplirse dos condiciones básicas:
Parsimonia e Interpretabilidad.
Parsimonia, los
fenómenos deben explicarse con el menor número de elementos posibles. Por lo
tanto, respecto al Análisis Factorial, el número de factores debe ser lo más
reducido posible y éstos deben ser susceptibles de interpretación substantiva.
Una buena solución factorial es aquella que resulta sencilla e interpretable.
Los pasos o fases que se suelen seguir en el Análisis Factorial son los
siguientes:
1. Cálculo de la
matriz de correlaciones entre todas las variables (conocida habitualmente como
matriz R).
2. Extracción de
los factores necesarios para representar los datos.
3. Rotación de
los factores con objeto de facilitar su interpretación.
4.
Representación gráfica.
5. Cálculo de
las puntuaciones factoriales de cada individuo.
Realización de un
Análisis Factorial:
-FORMULACIÓN DEL PROBLEMA.
·
-ANÁLISIS DE LA MATRIZ DE CORRELACIÓN.
·
-EXTRACCIÓN DE FACTORES.
·
-DETERMINACIÓN DEL NÚMERO DE FACTORES.
·
-ROTACIÓN DE FACTORES.
·
-INTERPRETACIÓN DE FACTORES.
·
-VALIDACIÓN DEL MODELO.
·
-CÁLCULO DE PUNTUACIONES.
SEGÚN LA TGS:
El análisis factorial explica el
aislamiento por medio del análisis matemático de los factores, en aquellos
problemas caracterizados por ser multivariables.
TEORÍA DE LA
DECISIÓN:
Es saber escoger
gracias a conocimientos habilidades técnicas y artísticas adquiridas o a la
experiencia entre varias alternativas para satisfacer las metas contenidas en
una estrategia.
La decisión es
efectiva o eficiente, cuando satisface en la totalidad, o al menos en un alto
porcentaje, el objetivo o fin deseado y en el momento oportuno en que la
decisión debe ser tomada.
Casi no es posible
imaginar un campo de mayor tracendencia para el humano que el de la toma de
decisiones. Tenemos un problema cuando no sabemos como seguir. Una vez que
tenemos un problema, hay tomar una decisión. Elegimos una alternativa que nos
parezca suficientemente racional que nos permita mas o menos maximizar el valor
esperado luego de resuelta nuestra acción. Emitimos en silencio un plan de
control, que nos ayuda en la toma de decisiones. incluyendo decisiones
relacionadas con modificar ese plan de control. Demostramos nuestra
inteligencia en este proceso en funcionamiento.
La toma de
decisiones es también una ciencia aplicada que ha adquirido notable importancia
y es el tema básico de la Investigación Operativa.
Muchas personas
todavía están bajo el cautiverio de la tutela auto contraida. La tutela es la
incapacidad de la persona de tomar sus propias decisiones. Y es auto contraida
cuando su causa no es la falta de razón sino la falta de resolución y coraje
para usarla sin desear que nos diga qué hacer alguna otra persona.
CARACTERÍSTICAS Y
FACES DEL PROCESO DE DECISIÓN
1) Existen al menos
dos posibles formas de actuar, que llamaremos ALTERNATIVAS o ACCIONES,
excluyentes entre sí, de manera que la actuación según una de ellas
imposibilita cualquiera de las restantes.
2) Mediante un
proceso de decisión SE ELIGE UNA ALTERNATIVA, que es la que se lleva a cabo.
3) La lección de un
alternativa ha de realizarse de modo que cumpla un FIN determinado.
El proceso de decisión
costa de las siguientes FASES fundamentales:
* Predicción de las
consecuencias: de cada actuación. Esta predicción deberá basarse en la
experiencia y se obtiene por inducción sobre un conjunto de datos. La
recopilación de este conjunto de datos y su utilización entran dentro del campo
de la Estadística
* Valoración de las
consecuencias: de acuerdo con una escala de bondad o deseabilidad. Esta escala
de valor dará lugar a un sistema de preferencias
* Elección de las
consecuencias: mediante un criterio de decisión adecuado. Este punto lleva a su
vez asociado el problema de elección del criterio más adecuado para nuestra
decisión, cuestión que no siempre es fácil de resolver de un modo totalmente
satisfactorio.
Explicación de
la temática de la teoría de la decisión.
La temática de
la teoría de la decisión, implica necesariamente la aplicación a la práctica,
constante, sistemática y regular en todos los temas.
La Teoría de la
decisión se basa en el principio según el cual el sujeto decisor debe elegir la
alternativa preferida. El problema consiste en que, muchas veces, no puede
decir cuál de dos alternativas prefiere, impedimento cuya dificultad se
incrementa debido a que tales alternativas, al referirse a un tiempo futuro,
son inciertas. Teoría de la Decisión es quizás la única materia definitivamente
teórica que encontrará el estudiante en su carrera. Esa característica
consiste, no en estar alejada de la práctica, bien al contrario, sino en
articular los elementos, los conceptos, los criterios y los métodos de
raciocinio, de reflexión, de pensamiento organizado y sistemático destinado a
hallar la mejor solución a una situación dada.
La teoría de la
decisión aplicada correctamente asegura “una mejor decisión”, calificando a los
procedimientos, y no a sus resultados. (no por su éxito). La temática de la
teoría de la decisión, implica necesariamente la aplicación a la práctica,
constante, sistemática y regular en todos los temas que la componen. La
transmisión del conocimiento no puede efectuarse en el marco de la definición
teórica, sin su correlato en la vida diaria, ya sea de las organizaciones o del
decisor individual.
Ejemplo
*Suponga que
usted compra a $1.000 un número de una rifa, la cual paga un premio de $50.000.
*Hay dos eventos
posibles:
- Usted gana la
rifa, o
- Pierde
*¿Cuál es el
valor esperado del juego?
* La
distribución de probabilidades es:
* El valor
esperado es:
49000*(1/100)+-1000*99/100=-500
* ¿Qué significa
ese resultado?
* Puede usarse
para desarrollar una estrategia óptima cuando el tomador de decisiones se
enfrenta con:
- Una serie de
alternativas de decisión.
- Incertidumbre
o eventos futuros con tiesgo.
*/ Un buen
análisis de decisiones incluye un análisis de riesgo.
RELACIÓN CON LA
TGS.
La toma de
decisiones en las organizaciones es un proceso complejo que esta estrechamente
relacionado con las dimensiones de estructura, interacción, comunicación, poder
y cultura.
CIBERNETICA:
Ciencia que
estudia los mecanismos de comunicación, regulación y control de sistemas
complejos, especialmente sistemas informáticos.
La cibernética
es una ciencia, nacida hacia 1948 e impulsada inicialmente por Norbert Weiner
que se ocupa de los sistemas de control y de comunicación en las personas y en
las máquinas, estudiando y aprovechando todos sus aspectos y mecanismos
comunes.
VENTAJAS DE LA
CIBERNÉTICA.
La reducción de
las jornadas laborales; los trabajos complejos o rutinarios pasarían a ser de
las máquinas.
DESVENTAJAS DE
LA CIBERNÉTICA.
Reemplazo de
mano de obra humana por mano de obra robótica.
Eventualmente
aumentaría la desigualdad social.
Los países más
industrializados ejercerían un control aun mayor sobre los países menos
tecnología.
ROBÓTICA.
Es la ciencia
que trata acerca del diseño y la implementación de maquinas capaces de emular
el comportamiento de un ser vivo.
CAMPO DE ACCIÓN
DE LA CIBERNÉTICA.
Dentro del campo
de la cibernética se incluyen las grandes máquinas calculadoras y toda clase de
mecanismos o procesos de autocontrol semejantes y las máquinas que imitan la
vida.
INTELIGENCIA
ARTIFICIAL Y LA BIÓNICA
La biónica es
aquella rama de la cibernética que trata de simular el comportamiento de los
seres vivos haciéndolos mejores en casi todas las ramas por medio de
instrumentos mecánicos.
la inteligencia
artificial es la disciplina que se encarga de construir procesos que al ser
ejecutados sobre una arquitectura física producen acciones o resultados que
maximizan una medida de rendimiento determinada.
PRINCIPIOS
BÁSICOS DE LA CIBERNÉTICA EN TGS:
Según la teoría
de la información, uno de los principios básicos de la cibernética establece
que la información es estadística por naturaleza y se mide de acuerdo con las
leyes de la probabilidad.
La conducta
intencionada en las personas o en las maquinas exige mecanismos de control que
mantengan el orden, contrarrestando la tendencia natural hacia el desorden.
TEORÍA DE LA
INFORMACIÓN:
La cibernética
ha sido considerada desde sus inicios como teoría de la información.
https://prezi.com/m4qfuyhpvhgc/cibernetica/
TEORÍA DE LA INFORMACIÓN:
Es la teoría relacionada con las leyes matemáticas que rige
la transmisión y el procesamiento de la información. Más concretamente, la
teoría de la información se ocupa de la medición de la información y de la
representación de la misma (como, por ejemplo, su codificación) y de la
capacidad de los sistemas de comunicación para transmitir y procesar
información.
El tipo de sistema de comunicación más estudiado consta de
varios componentes. El primero es una fuente de información (por ejemplo, una
persona hablando) que produce un mensaje o información que será transmitida. El
segundo es un transmisor (como, por ejemplo, un teléfono y un amplificador, o
un micrófono y un transmisor de radio) que convierte el mensaje en señales
electrónicas o electromagnéticas.
La teoría de la información también abarca todas las
restantes formas de transmisión y almacenamiento de información, incluyendo la
televisión y los impulsos eléctricos que se transmiten en las computadoras y en
la grabación óptica de datos e imágenes.
TEORÍA DE LA INFORMACIÓN COMO PRINCIPIO DE TGS.
La teoría de la información se podría ver como un principio
de la tgs porque sus dos autores principales tales como Lachman y Butterfield
se enfocaron en el en una teoría que se pudiera aplicar para toda las ciencias.
En este caso el procesamiento de información.
https://prezi.com/eruftfafkuqf/teoria-de-la-informacion/
TEORÍA DE LOS JUEGOS:
La teoría de juegos es un área de la matemática aplicada que
utiliza modelos para estudiar interacciones en estructuras formalizadas de
incentivos (los llamados juegos) y llevar a cabo procesos de decisiones Sus
investigadores estudian las estrategias óptimas así como el comportamiento
previsto y observado de individuos en juegos.
Un juego consiste en un conjunto de jugadores, un conjunto
de estrategias o movimientos, disponibles para esos jugadores y una
especificación de recompensas para combinación de estrategias.
En juegos de forma normal, los jugadores mueven
simultáneamente. Si el conjunto de estrategias es discreto y finito, el juego puede
ser representado por una matriz NxM.
Un juego en forma extensiva especifica el orden completo de
movimientos a través de la dirección del juego, generalmente en un árbol de
juego.
Los economistas han usado la teoría de juegos para analizar
un amplio abanico de problemas económicos, incluyendo subastas, duopolios,
oligopolios, la formación de redes sociales, y sistemas de votaciones.
Se usó por primera vez para explicar la evolución (y
estabilidad) de las proporciones de sexos 1:1 (mismo número de machos que de
hembras)
La teoría de los juegos se utiliza como definición del
pensamiento estratégico como arte de vencer al adversario sabiendo que
este está tratando de hacer lo mismo con
uno (supone un nivel de conflicto)
Una explicación de la teoría de la paz democrática es que el
debate público y abierto en la democracia envía información clara y fiable
acerca de las intenciones de los gobiernos hacia otros estados.
Muchas teorías lógicas se asientan en la semántica de
juegos. Además, los investigadores de informática han usado juegos para modelar
programas que interactúan entre sí.
TIPOS DE JUEGOS
Juegos simétricos:
Un juego simétrico es un juego en el que las recompensas por
jugar una estrategia en particular dependen sólo de las estrategias que empleen
los otros jugadores y no de quien las juegue.
Juegos asimétricos:
Los juegos asimétricos más estudiados son los juegos donde
no hay conjuntos de estrategias idénticas para ambos jugadores.
Juego de Suma cero:
En los juegos de suma cero el beneficio total para todos los
jugadores del juego, en cada combinación de estrategias, siempre suma cero (en
otras palabras, un jugador se beneficia solamente a expensas de otros).
Juego de suma no cero
Juegos de sumas no cero, porque algunos desenlaces tienen
resultados netos mayores o menores que cero. Es decir, la ganancia de un
jugador necesariamente no corresponde con la pérdida del otro.
Paradoja del prisionero
El dilema del prisionero es un juego que se basa en dos
supuestos: (1) Cada jugador tiene incentivos para elegir una alternativa que le
beneficie a él, pero que perjudica al contrario. (2) Cuando ambos jugadores
actúan de este modo, acaban en una situación peor que si hubieran decidido
alternativas diferentes.

https://prezi.com/krlvwwe5d5ug/teoria-de-los-juegos/?utm_campaign=share&utm_medium=copy













No hay comentarios:
Publicar un comentario